Tests & Statistik
Inhalt
- Ein Elefant, der nicht im Raum ist
- Was sagt ein Test aus?
- Medizinische Statistik
- Covid-19 Tests
Ein Elefant, der nicht im Raum ist
Was sagt uns „eine 95%ige Wirksamkeit?“
„Impfstoffe gegen Covid-19 sind hochwirksam“ heißt es. Wenn es so ist: Was bedeutet eigentlich „Wirksamkeit“? Vor allem: In Bezug auf was?
Was wurde in den Studien genau gemessen? Welche Unterschiede sollten bei Geimpften und Nicht-Geimpften mit gefunden werden: Schwere Krankheitsverläufe oder „Husten-Schnupfen-Heiserkeit“? Wie wurde Aussagekraft der genutzten PCR-Typ (hinsichtlich Genauigkeit und Empfindlichkeit) gemessen? Wie häufig konnte man bei einem positiven Covid-19-PCR-Test – je nach Durchseuchung der beobachteten Bevölkerungsgruppe – von einer Infektion mit einem lebendem Virus ausgehen?
Scheinbar eindeutiges ist manchmal weniger eindeutig,
wenn genauer hinsieht:
„Unkoordinierte Phase-3-Studien erfüllen nicht die Anforderungen des öffentlichen Gesundheitswesens. … Die Überlegungen zur Wirksamkeit und Effektivität basieren auf Studien, die die Vorbeugung von leichten bis mittelschweren COVID-19-Infektionen messen. Sie wurden nicht erdacht, um Aussagen zur Vorbeugung von Krankenhausaufenthalten, schweren Erkrankungen oder Todesfällen oder zur Vorbeugung von Infektionen und Übertragungspotenzialen zu treffen. Die Beurteilung der Eignung von Impfstoffen müsste alle Indikatoren berücksichtigen, und auch Sicherheit, Einsatzfähigkeit, Verfügbarkeit und Kosten einbeziehen.“ Olliario, Lancet 20. April 2021, Übersetzung: Jäger. Ein unterhaltsamer Versuch, diese mathematische Logik zu erklären Patrick Strobach 30.05.2021
Zu den Publikationen
- Olliario P et al.: Covid-19 vaccine efficacy & effectiveness – the elephant (not) in the room. The Lancet 20.04.2021 –
- Olliario P: What does 95% COVID-19 vaccine efficacy really mean? The Lancet 21.06.2021 –
- Gigerenzer G: „Unstatistik (RWI Essen) 02.12.2020“
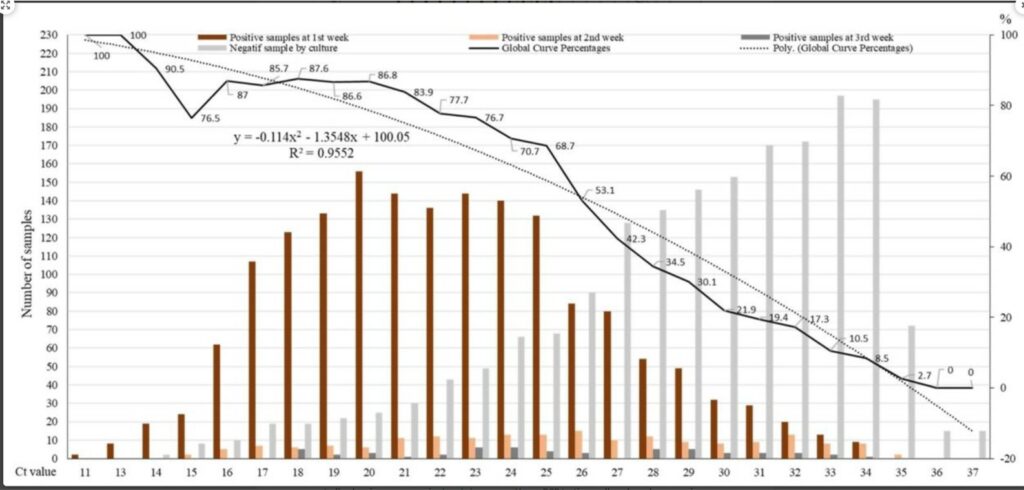
- Jafaar R: Correlation Between 3790 Quantitative Polymerase Chain Reaction–Positives Samples and Positive Cell Cultures, Including 1941 Severe Acute Respiratory Syndrome Coronavirus 2 Isolates, Clinical Infectious Diseases (CID) 21.06.2021:72
Die Aussagen dieser Publikationen sind nicht neu. Sie erklären nur die Unterschiede zwischen
- einem PCR-Test und einem virologischen Kulturverfahren.
- einem „Relativem Risiko“, das sehr groß erscheint, weil es auf kleine Teilgruppen bezogen wird. Und einem „Absoluten Risiko“ (in einer gesamtgruppe), das oft sehr klein ist.
Nur mit der einen Variante einer (sicher korrekten) Darstellung kann man Nicht-Statistiker:innen tief beeindrucken.
Mit der anderen gelänge das weniger gut.
Was sagt ein Test?
Tests erzählen von einer Wahrscheinlichkeit, mit der ein Ereignis eintreffen werde. Sie liefern bestensfalls Momentaufnahmen von Einzelereignissen. Und sagen nicht aus, „Wie es ist“ oder „Wie es nicht ist“.
Bevor Blut abgenommen wird, um einen Tumormarker zu bestimmen, es wäre günstig, das zu wissen.
Eigentlich ist es ganz einfach
Im 18. Jahrhundert hatte der Pfarrer und Hobbymathematiker Thomas Bayes etwas Geniales herausgefunden: Höre man in London Hufgetrappel, kündige dasmeistens ein Pferd an. Seltener vielleicht auch einen Esel. Aber:
„Wenn du Hufgetrappel hörst, glaube nicht ein Zebra käme um die Ecke!“
Das klingt banal, ist es aber nicht.
Denn es bedeutete, dass man nicht nur mit dem rechnen sollte, was ein Sinneseindruck vermittelt (oder ein Test als Resultat bringt). Sondern ebenso mit dem, was (aus Erfahrung) wahrscheinlich zutreffen könnte.

Bayes Calculator
Bayes hatte entdeckt, dass die Wahrscheinlichkeit des Eintritts eines konkreten Ereignisses u.a. von einem subjektiven Glauben abhängt. Für die Beurteilung einer Sinnesmeldung (oder eines Tests) ist Überzeugung notwendig, wie groß die Wahrscheinlichkeit sei, dass ein solches Ereignis in einem größeren Zusammenhang überhaupt vorkommen könne.
Der Glaube an die Wahrscheinlichkeit eines Ereignisses kann entweder auf Erfahrung beruhen („Ich habe noch nie ein Zebra in London gesehen“), oder auf Hörensagen: („Man sagt mir, es gäbe keine Zebras in London“).
Vor Bayes hatte nicht fassbare Subjektivität nichts in der Naturwissenschaft suchen.
Inzwischen wurde aber selbst die Physik von dem „subjektivistischen“ Gift des Pfarrers Bayes infiziert (Fuchs 2012, Fuchs 2010). In der Physik sind Entweder-Oder-Ereignisse eher selten. Viel häufiger werden Wissenschaftler*innen mit unklaren Situationen konfrontiert, die zudem davon abhängen, wie sie betrachtet werden. Mit Bayes Erkenntnissen schlich sich erstmals Subjektivität in die nüchterne, scheinbar objektive Mathematik.
Die Annahme, dass etwas nicht sicher, sondern nur wahrscheinlich sein könnte, nährt sich aus Erlerntem, Gelesenem, Gehörtem und natürlich aus eigener Erfahrung. Eine Ansicht, dass etwas bei einer sehr großen Zahl von Beobachtungen so sei, bleibt nützlich. Mehr nicht. In anderen Situationen, bei anderen Beobachtern und bei anderen Formen der Betrachtung könnte es ganz anders gesehen werden.
Tests werden durchgeführt, um eine Situation Welt sei berechenbar und verfügbarer zu machen. Die Bayes Test-Logik führt aber wieder in die Unsicherheit und die Unverfügbarkeit zurück.
Viele Ärzt*innen mögen das nicht. Weil sie gelernt haben, „wie es wirklich ist“, undihren Patient*innen Sicherheit vermitteln wollen. Deshalb vergessen sie rasch ihre Zweifel und die Grundlage der Statistikkurse, mit denen sie im Studium gequält wurden.
Stattdessen zapfen sie ihren Patient*innen viel Blut ab, um sie auf alles Mögliche zu testen. Denn das produziert (scheinbar) sichere und eindeutige Ergebnisse. Ist einer der vielen Tests dann positiv, scheint das Rätsel der Krankheit gelöst zu sein. So einfach ist das.
Würden sie sich dagegen an Bayes erinnern, würden sie wesentlich seltener testen.
„Lasse den Zuschauer nie im Ungewissen,
Alfred Hitchcock
sondern versorge ihn ständig mit Informationen,
die ihn weiter verunsichern.“
Im Gesundheitsmarkt orientiert man sich gerne an Hitchcocks Empfehlung: Denn, je bedrohlicher eine Situation erscheint, desto mehr mehr unklare Informationen strömen ein. Das erzeugt Angst, ein Gefühl das nach Sicherheit verlangt. Also einen starken Bedarf erzeugt, nach einem Produkt oder einem Ritual, „das alles wieder gut macht“.
Der nicht-aufgeregte Umgang mit Risiken erscheint dann „unlogisch“. Denn es könnte sich herausstellen, dass ein Risiko, dass sich eindeutig klein oder groß „anfühlt“, in der Realität erheblich anders geartet ist.
Bayes Statistik und die lebendige Bewegung
Nicht nur Statistiker rechnen mit der Logik des alten Pfarrers Bayes , sondern alle Lebewesen (Körding 2006):
Tiere gleichen bei allen Ereignissen, die ihnen begegnen, die Meldungen der Sinnesorgane mit ihrer Erfahrung ab. Die einströmenden Information, melden nur Teilaspekte und sind zudem durch Rauschen überlagerte. Sich auf solche ungenauen Daten zu verlassen könnte tödlich enden. Deshalb trainieren Säugetiere ihre Vorhersagefähigkeiten, und werden mit anwachsender Erfahrung immer erfolgreicher.
Denn für effektive Bewegungen (z.B. Tennisspielen) reichen die Sinnes-Informationen nicht aus: Sie sind zu unscharf, täuschen und verbergen vielleicht das Wichtigste (den Spin des anfliegenden Balls). (Bain 2016, Wolpert 2016)
Bevor man gelöst und locker spielen kann, muss durch geduldiges Training ein Erfahrungsschatz aufgebaut werden. Daraus ensteht ein Sicherheitsgefühl, zu wissen, wie Bälle, die in einer bestimmten Art anfliegen, sich wohl verhalten würden. Die Bewegung baut also nur zum Teil auf der unmittelbaren Information auf. Sie erfordert ebenso die Einschätzung der Gesamtsituation, aufgrund subjektiver Erfahrung.
Diese Erkenntnis verstörte viele Biologen und Hirnforscher, die Bewegungsroboter konstruieren wollten. Denn offenbar sind Nerven- und Bewegungszellen nur Teile lebender Schwingungskreise, die für sich allein nicht sinnvoll funktionieren können.
Bayes-Logik
- An Intuitive Explanation of Bayes‘ Theorem (Yudkovsky)
- Bain R: Are our brains Baysian? Significance 8/2016:14-19
- Bayes Calculator
- Bayes T (1763): Essay Towards Solving a Problem in the Doctrine of Chances. Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, M. A. and F. R. S.
- Körding KP: Bayesian decision theory in sensorimotor control, Trends in Cognitive Sciences, Special Issue: Probabilistic models of cognition. 2006, 10(7)P319-326,
- Wolpert D: Why do we have brains? 2016
Intelligenter Umgang mit Statistik und Wahrscheinlichkeiten
- Beck Bernholdt HP, Dubben HH bei rororo: (1) Der Hund der Eier legt – Erkennen von Fehlinformationen durch Querdenken. (2) Der Schein der Weisen – Irrtümer und Fehlurteile im alltäglichen Denken. (3) Mit an Wahrscheinlichkeit grenzender Sicherheit – Logisches Denken und Zufall
- Bauer T et al.: Warum dick nicht doof macht und Genmais nicht tötet – Über Risiken und Nebenwirkungen der Statistik, Campus 2014
- Dobelli R: Die Kunst des klaren Denkens – 52 Denkfahler. Hanser 2011
- Dörner D: Die Logik des Mißlingens, Strategisches Denken in komplexen Situationen, rororo 2003
- Gigerenzer G.: Einfache Regeln für komplexe Entscheidungen. 2017 ; Das Einmaleins der Skepsis: Über den richtigen Umgang mit Risiken und Zahlen, Berliner Taschenbuch Verlag, 2002 ; Harding Center für Risiko-Kompetenz
- Mühlhauser I: Unsinn Vorsorgemedizin, Okt 2017, rororo, www.brustkrebs.info
Medizinische Statistik
Angesichts von Zahlenkolonnen reagieren viele hilflos ..
.. und ziehen vorschnelle Schlüsse.
Beispiel Brustkrebs
Der Risikoforscher Gigerenzer (s.u.) fragte, wie groß die Wahrscheinlichkeit sei, dass eine Frau mit einem gerade festgestellten, verdächtigen Mammographie-Befund an Brustkrebs leide. Etwa 15% befragter Ärztinn/en fanden die richtige Antwort.
Die meisten gaben an, die Brustkrebs-Wahrscheinlichkeit für Frauen mit positivem Mammographie-Befund liege bei etwa 70-80%. Tatsächlich leiden aber nur etwa 10% der Frauen mit einem verdächtigen Mammographie-Befund an Brustkrebs.
Wie kann das sein?
Bei etwa 1% aller Frauen im Alter über 40 Jahren besteht ein Mammakarzinom. Bei einer Vorsorgeuntersuchung würde es mit einer Wahrscheinlichkeit von 80-90% erkannt werden. Bei mindestens 10% würde der Test aber negativ ausfallen, obwohl eine Erkrankung vorliegt.
99% der Frauen, die zu einer Vorsorgeuntersuchung gehen, leiden nicht an Brustkrebs. Aber bei 10% dieser gesunden Frauen würden sich in einer Mammographie Hinweise auf eine mögliche Krebserkrankung finden.
Bei 10.000 untersuchten Frauen haben
- 80 Frauen Brustkrebs und eine auffällige Mammographie (Gruppe A)
- 20 Frauen Brustkrebs, und keine auffällige Mammographie (Gruppe B)
- 950 Frauen keinen Brustkrebs, aber eine auffälliger Mammographie (Gruppe C)
- 8.950 Frauen keinen Brustkrebs und eine unauffällige Mammographie (Gruppe D)
In der Gruppe mit positiven Mammographie-Befund (A+C) liegt die Rate der erkrankten Frauen in diesem Beispiel bei 7,8% (A x 100 / (A+C) ).
Die Zahl 7,8 (der „positive Vorhersagewert“) vermittelt, wie viele positiv Getestete tatsächlich krank sind. Der „negative Vorhersagewert“ zeigt den Anteil der negativ Getesteten, die tatsächlich gesund sind (im Beispiel: 99,78%), d.h. bei 22 von 10.000 negativ-getesteten Frauen würde trotz des Testes ein Brustkrebs vorliegen.
Würde die Zahl der „falsch-negativen“ Tests durch immer genauere Methoden drastisch gesenkt werden, müsste zwangsläufig die Zahl der „falsch-positiven“ Tests ansteigen.
Die Risiken und der Nutzen von Früherkennungsuntersuchungen und Vorbeugungsmaßnahmen sind nicht einfach zu verstehen.
Besonders, wenn die Ergebnisse der Statistik dem „gesunden Menschenverstand“ oder dem „Bauchgefühl“ widersprechen (als paradox oder kontraintuitiv empfunden werden).
Risikoforscher, die sich mit diesen Zusammenhängen beschäftigen, beklagen eine fehlende, ärztliche Statistik-Kompetenz.
Screening-Methoden würden zunehmend zur juristischen Absicherung eingesetzt, „um nichts zu übersehen“. Und oft würden Methoden, deren Risiken den Nutzen übersteigen, unkritisch (wider besseres Wissen) angewandt werden (Mühlhauser 2017).
Das was Medizin-Statistiker (s.u.: Gigerenzer, Beck-Bornhold&Dubben, Mühlhauser) und auch mich zur Verzweiflung bringt, ist, dass nur extrem wenige im Medizin-Business die Test Logik verstehen. Mit Risiken und Test-Systemen wird nämlich meist nicht rational, sondern emotional-kommerziell umgegangen.
Die Statistiker wiederum glauben,
sie wüssten wie es ist, und wenn man dieses Wissen nur einfach genug aufbereite, müsse es jede/er verstehen. Beides ist falsch.
Statistisch fassbare Daten beziehen sich immer nur auf wenige Faktoren eines Gesamtsystems. Damit Messungen exakt ausfallen, werden dafür alle anderen (oder die große Mehrzahl) der beteiligten Faktoren ausgeschlossen. Es werden Bedingungen geschaffen, die die „störenden“ Wechselwirkungen und Beziehungen der realen Welt bei der Beobachtung beseitigen.
Der direkte Rückschluss von Experimenten, die Messdaten liefern, auf die Realität einer Patienten-Situation wäre deshalb irreführend.
Die Erkenntnisse statistischer Daten sind nicht auf konkrete Situationen übertragbar.
Das Wissen, dass wir überwiegend „nicht-wissen“ verunsichert. Und die Produktion vieler Daten ändert daran im Prinzip nichts. Denn alle Studien können nicht belegen, was gut und richtig „ist“, sondern nur anregen, auf der Basis der neu gesammelten Informationen klügere Fragen zu stellen, nach dem wie sich etwas entwickeln könnte.
Menschen aber, die sich gerade durch Schmerzen bedroht fühlen, sehnen sich nach Rettung, und können daher nicht sorgfältig „Für und Wider“ abwägen. Auch bei Trauer, Sorge Angst, Ekel, Ärger oder Wut ist die emotionslose Rationalität der Zahlen nicht nachvollziehbar.
Bevor also statistische Informationen auf einfache, verständliche Art bildhaft vermittelt und bewertet werden, müssen Patientinn/en in der Lage sein, rationale Informationen auch verarbeiten zu können. Patientinn/en können nur dann gut mit Zweifel umgehen, wenn ihnen zuvor in einer vertrauensvollen Arzt-Patient-Beziehung die Angst genommen wird. Wenn sie das Gefühl haben, in einem Vertrauensverhältnis gut aufgehoben zu sein.
Vor der Übersetzung statistischer Informationen muss sich also eine menschliche Beziehung entwickeln
Kompetente Expertensicht
- Methodenwissen (z.B. zu Möglichkeiten und Grenzen der Statistik)
- Kenntnis reiner Fakten (Daten: „nackte Zahlen“)
- Spielraum der Interpretation reiner Fakten: Hinweise für überprüfbare Evidenz und Wissen, was nicht bekannt ist
- Aktuelle Mehrheits-Interpretation (Leitlinien) und qualifizierte Minderheits-Interpretation (widersprechende Studien)
- Rationale Interpretation (logische und skeptische Sprachen)
Kompetente Betroffenensicht
- Persönliche Zusammenhänge: Lebenssituation, körperlich-psychisches Empfinden, Lebensweg
- Bedeutung des einzelnen (z.B. des Problems) für „das Ganze“, z.B. für den Beziehungszusammenhalt
- Bedürfnisse, Ressourcen, Selbstwert, Möglichkeiten, Ziele, Visionen
- Wertesystem und Schwerpunktsetzungen hinsichtlich Lebensqualität und Lebenszeit
- Emotionale Interpretation wortlos gefühlter Kommunikation
Expert*innen können zu Betroffenen werden und mit ihnen fühlen.
Sie könnten den Betroffenen helfen, sich zu Expertinn/en entwickeln, die damit beginnen selber zu denken. Das Denken auf der Basis statistischer Daten kann sehr wirksam sein, um den Unsinn in der Medizin zu erkennen. Rationaler Zweifel muss aber eingebettet sein in menschlich fühlende Beziehungen.
Zuviel Information, die nicht sinnvoll in einen persönlichen Zusammenhang eingeordnet werden kann, verstärkt Ängste, und führt zu Abwehr, Tunnelblick und irrationalem Handeln.
Frau Mühlhauser beklagt daher zurecht, dass es Menschen, die leiden oder die Angst verspüren, an „risk literacy“ mangelt. Darunter versteht sie die Fähigkeit, Risiken zu verstehen und für sich selbst abwägend beurteilen zu können. Wenn diese Kompetenz nur schwach entwickelt ist, sind Patientinn/en den Überangeboten der Gesundheitswirtschaft ziemlich hilflos ausgeliefert.
Bereits vor 2.500 Jahren soll ein griechischer Arzt empfohlen haben, dass der, der ein Beim
amputieren kann, nicht der sein darf, der entscheidet, dass das Bein abgeschnitten wird. In der modernen Gesundheitswirtschaft gewinnt dieses Prinzip erheblich an Bedeutung.
„Unabhängige Beratung muss möglich sein!“ Ingrid Mühlhauser 2017
.. damit es Patientinn/en ermöglicht wird, eigene, rationale, selbstbewusste
Entscheidungen zu treffen und weniger Blödsinn zu konsumieren. (Sirovich 2004, Smith 2004)
Video
- MDR „Fakt ist …“ 14.07.2014
- BR „Wie Statistiken unser Leben lenken“ 26.11.2013
- Gigerenzer: Einfache Regeln für komplexe Entscheidungen. 2017
Literatur
- Beck Bernholdt HP, Dubben HH bei rororo: (1) Der Hund der Eier legt – Erkennen von Fehlinformationen durch Querdenken. (2) Der Schein der Weisen – Irrtümer und Fehlurteile im alltäglichen Denken. (3) Mit an Wahrscheinlichkeit grenzender Sicherheit – Logisches Denken und Zufall
- Bauer T et al.: Warum dick nicht doof macht und Genmais nicht tötet – Über Risiken und Nebenwirkungen der Statistik, Campus 2014
- Dobelli R: Die Kunst des klaren Denkens – 52 Denkfahler. Hanser 2011
- Dörner D: Die Logik des Mißlingens, Strategisches Denken in komplexen Situationen, rororo 2003
- Gigerenzer G.: Vortrag: Einfache Regeln für komplexe Entscheidungen. 2017 ; Das Einmaleins der Skepsis: Über den richtigen Umgang mit Risiken und Zahlen, Berliner Taschenbuch Verlag, 2002 ; Harding Center für Risiko-Kompetenz
- Mühlhauser I: (1) Unsinn Vorsorgemedizin, Okt 2017, rororo (2) Mammograhie Screening für Frauen ab 70? https://arbeitskreis-frauengesundheit.de/2020/10/04/mammographie-screening-fuer-frauen-ab-70 (3) Screening auf Brustkrebs/Mamographie-Screening, Deutsche Zeitschrift für Onkologie 2013, 45:80-85
- Sirovich BE: Cervical Cancer Screening Among Women without a Cervix, JAMA, June 2004, 291, 24:2990-2993.
1992 wurde in den USA bei fast 68% der Frauen nach vollständiger Gebärmutterentfernung eine Gebärmutterhalskrebs-Vorsorgeuntersuchung durchgeführt. 1996 empfahlen dann Fachleitlinien, das künftig zu unterlassen. 2002 erfolgte dann diese Vorsorgeuntersuchung bei 69% von Frauen ohne Gebärmutterhals. - Smith R: Abusing patients by denying them choice BMJ 2004 Feb 14; 0. BMJ-Editorial 14.02.2004, 328(7436):
Bei Screening-Optionen bzgl „Rektum-Krebs“ entschieden sich nach Aufklärung über Nutzen und Risiken 87% aller Patientinn/en gegen invasive Verfahren
Covid-19 – Test
25.11.2020
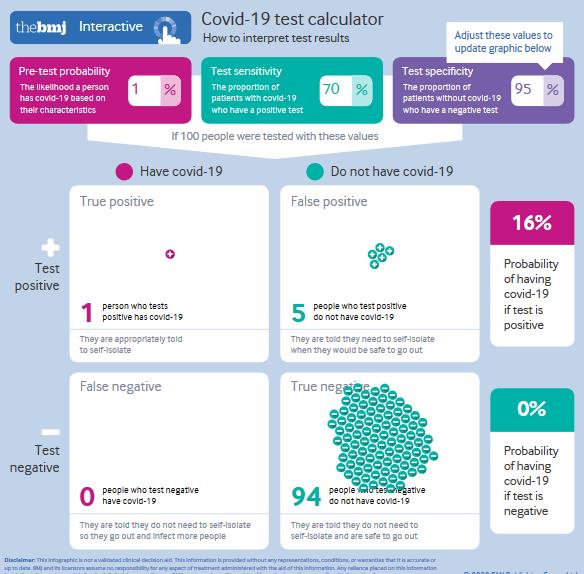
Die Aussagekraft von Tests ist begrenzt.
Früher galt jemand als gesund oder krank, weil er oder sie sich so fühlte. Heute: weil ein Test positiv oder negativ ausfällt.
Die Qualität der Vorhersage eines Tests hängt von vielem ab. Nicht nur von technischen Faktoren ab. Sondern auch von der Wahrscheinlichkeit des Auftretens der Ereignisse, die gemessen werden sollen. (Schlenger 2020)
Um Testergebnisse beurteilen zu können, muss man die Wahrscheinlichkeit kennen, mit der ein Test
- tatsächlich vorliegende Infektionen entdecken (Sensitvität), und
- bei fehlenden Infektionen falsch-positiv ausfallen (Spezifität).
Zudem hängt die Wahrscheilichkeit, ob ein Test richtig oder falsch positiv ist, auch von der Häufigkeit des Ereignisses in der untersuchten Bevölkerungsgruppe ab (z.B ob ernsthaft Erkrankte oder gesunde Testpersonen untersucht werden).
Die WHO hat Rückmeldungen von Anwendern über ein erhöhtes Risiko für falsche SARS-CoV-2-Ergebnisse bei der Untersuchung von Proben mit RT-PCR-Reagenzien .. erhalten. WHO has received user feedback on an elevated risk for false SARS-CoV-2 results when testing specimens using RT-PCR reagents on open systems. WHO Warnung am 17.12.2020
Meldezahlen sind wenig verlässlich (Schrappe 17.12.2020). Es ist meist undurchschaubar
- welche Daten,
- nach welcher Konzeption,
- nach welchen Kriterien,
- mit welcher Technik,
- in welcher Bevölkerungsgruppe,
- mit welchem Ziel,
- von wem erhoben,
- von wem ausgewertet wurden, und
- wer diese Maßnahmen koordiniert und
- wer die Ergebnisse (wie sorgfältig) gemeldet hat.
Unsicherheit erzeugen
„Lasse den Zuschauer nie im Ungewissen,
sondern versorge ihn ständig mit Informationen,
die ihn weiter verunsichern.“ Alfred Hitchcock
Im Gesundheitsmarkt orientieren sich viele an Hitchcocks Empfehlung: Je mehr unklare Einzel-Informationen einströmen, desto bedrohlicher erscheint eine Situation.
Das erzeugt Dauer-Angst, ein sehr unangenehmes Gefühl, das dringend nach Sicherheit verlangt. Und so einen starken Bedarf erzeugt, nach einem Produkt oder einem Ritual, „das alles wieder gut macht“.
Im Panik-Tunnel ist keine Zeit für eine nicht-aufgeregte Beurteilung einer Gefahr. Wichtig ist dann nur, wie das Risiko, das sich bedrohlich groß anfühlen muss, beseitigt werden kann.
Wenn du störrische Hammel treiben willst, mach ihnen Angst vor dem Wolf. Alte Schäfer-Weisheit.
Extern
- Unstatistiken (RWI-Essen) –
- Das RKI zählt am Gesetz vorbei. Ansgar Neuhof ,14.09.2020 –
- „Etwa die Hälfte der Corona-Infizierten ist ansteckend“ Olfert Landt (PCR-Test-Hersteller, 06.01.2021) –
Zum Covid-19 Test
„Die (PCR-) Methode ist so empfindlich, dass sie ein einzelnes Erbmolekül dieses Virus nachweisen kann. Wenn ein solcher Erreger zum Beispiel bei einer Krankenschwester mal eben einen Tag lang über die Nasenschleimhaut huscht, ohne dass sie erkrankt oder sonst irgend etwas davon bemerkt, dann ist sie plötzlich ein Mers-Fall. Wo zuvor Todkranke gemeldet wurden, sind nun plötzlich milde Fälle und Menschen, die eigentlich kerngesund sind, in der Meldestatistik enthalten. Auch so ließe sich die Explosion der Fallzahlen … erklären. Prof Christian Drosten, Mai 2014, Wirtschaftswoche
Wenn es Anfang 2020 keinen PCR-Test gegen SARS-Cov-2 gegeben hätte?
Dann hätte man in Deutschland und einigen anderen Ländern nicht viel bemerkt

In vielen anderen europäischen Länder waren die Daten zur Übersterblichkeit allerdings ungewöhnlich:

Man hätte also
- im Winter 2019/2020 eine schwache „Grippewelle“ aufgezeichnet,
- im Frühjahr dann aber eine vermehrte Sterblichkeit an Atemwegsinfektionen vorwiegend bei älteren Menschen beobachtet, und besonders bei alten und mehrfach erkrankten Personen (nicht aber bei Personen unter 45 Jahren und Kindern),
- vermehrt Antikörpertestuntersuchungen durchgeführt. Die hätten aber nur wenig Klarheit gebracht. Möglicherweise hätten Virologen einen ungewöhnlichen Anteil der üblichen Coronaviren im Mix der Grippeviren beobachtet.
- in den Kliniken gesehen, dass Patienten einen untypischen „Influenza“-Verlauf durchmachten, und man sie ggf. anders behandeln muss (z.B. sie nicht so schnell beatmen sollte),
- die Verstorbenen auf Influenza getestet, und die Test-positiven als Influenzatote gezählt (so wie immer),
- die Ereignisse als eine (etwas zeitlich ungewöhnlich verzögerte), plötzlich ansteigende und ebenso schnell abfallende, heftige Grippewelle beurteilt, bei der die „Grippeimpfung“ (wieder einmal) keinen besonderen Schutz geboten hätte (siehe Euromomo-Daten 49 KW),
- im Sommer solange keine „zweite Welle“ beobachtet, wie die Sterblichkeitszahlen auf dem normalen Niveau geblieben wären. (Euromomo)
- wie jedes Jahr im Oktober In Deutschland wieder damit geworben, sich erneut mit einem neuen Influenza-Impfstoff gegen „Grippe“ impfen zu lassen, um „sicher gegen Grippe geschützt zu sein“.
- Und im November hätte man gesehen, dass die Zahl der Todesfälle (auch bei den Influenzgeimpften, ansteigt (Todesfälle/Infektion 2020). Obwohl der Index der Atemwegserkrankungen (nach Meldungen von Beobachtungspraxen) sehr niedrig blieb (RKI AG Influenza, abgerufen am 17.12.2020)
